plot_decision_boundary(tree1,axis=[-1.5,2.5,-1,1.5])

老师 绘图函数是使用的课件里面的绘图函数为什么绘制结果没有点呢，只有分界？

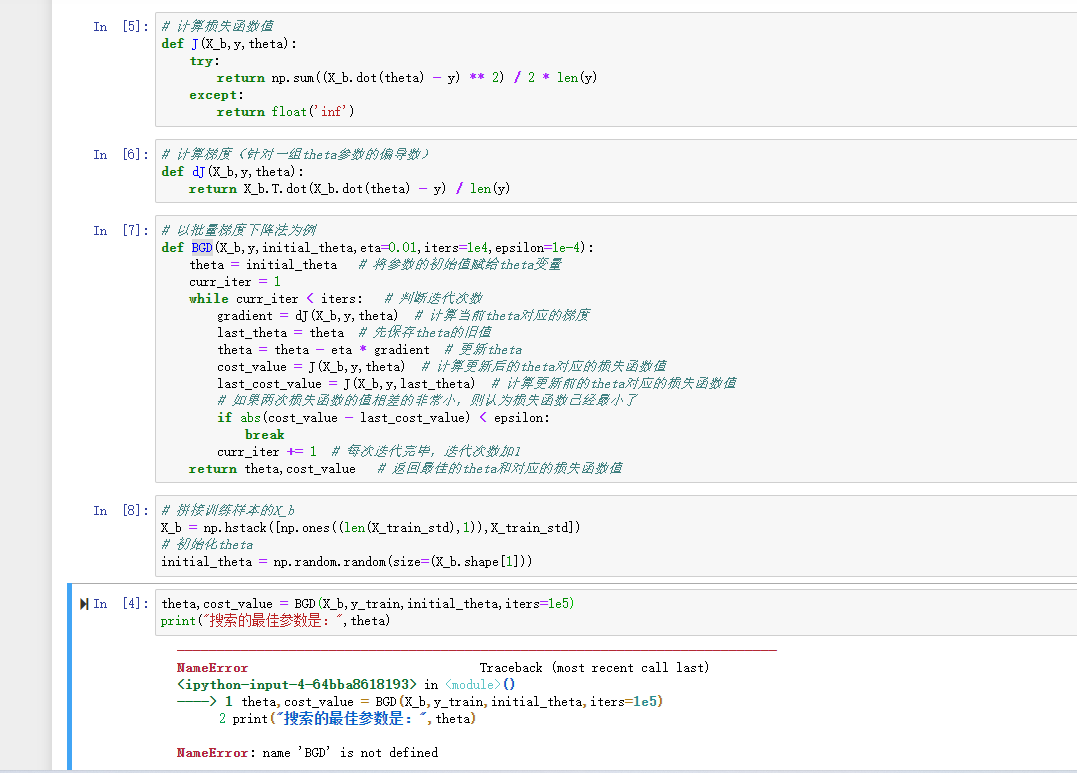
# 以批量梯度下降法为例
def BGD(X_b,y,initial_theta,eta=0.01,iters=1e4,epsilon=1e-4):
    theta = initial_theta   # 将参数的初始值赋给theta变量
    curr_iter = 1
    while curr_iter < iters:   # 判断迭代次数
        gradient = dJ(X_b,y,theta)  # 计算当前theta对应的梯度
        last_theta = theta  # 先保存theta的旧值
        theta = theta - eta * gradient  # 更新theta
        cost_value = J(X_b,y,theta)  # 计算更新后的theta对应的损失函数值
        last_cost_value = J(X_b,y,last_theta)  # 计算更新前的theta对应的损失函数值
        # 如果两次损失函数的值相差的非常小，则认为损失函数已经最小了
        if abs(cost_value - last_cost_value) < epsilon:
            break
        curr_iter += 1  # 每次迭代完毕，迭代次数加1
    return theta,cost_value   # 返回最佳的theta和对应的损失函数值
# 拼接训练样本的X_b
X_b = np.hstack([np.ones((len(X_train_std),1)),X_train_std])
# 初始化theta
initial_theta = np.random.random(size=(X_b.shape[1]))
theta,cost_value = BGD(X_b,y_train,initial_theta,iters=1e5)
print("搜索的最佳参数是：",theta)

如果在此基础上标准化

std = StandardScaler()
X_train_standard = std.fit_transform(X_train)
X_test_standard = std.transform(X_test)

# 标准化以后再代入调好的超参数
best_knn2 = KNeighborsClassifier(weights="distance",n_neighbors=2,p=2)
best_knn2.fit(X_train_standard,y_train)

y_predict = best_knn2.predict(X_test_standard)
print(y_predict)

# 分类准确率
sum(y_test == y_predict) / len(y_test)
# 直接调用score方法，得出分类准确率
print(best_knn2.score(X_test_standard,y_test))

为什么标准化和不标准化的分类准确率不一样呢

为什么在这节课样本特征标准化跟上一节不一样啊，上一节是三行代码，这节课一行代码就可以了？

这个过拟合现象只是通过图像肉眼观看的么？是不是有什么方法或者函数具体点。

这里用confusion_matrix混淆矩阵的目的是啥？

model1=AdaBoostClassifier([DecisionTreeClassifier(max_depth=5,max_leaf_nodes=10),LogisticRegression(multi_class='multinomial')],n_estimators=50)

老师 在AdaBoost中只可以使用一个基模型吗?

老师 如何在AdaBoost中同时使用多个基模型？

老师 第一棵树的残差是实际值与预测值的差，之后决策树的残差是当前决策树的预测值与上一棵树的残差之差，当残差为0的时候，下一颗树就不会再对该节点的残差进行计算，那么当所有节点的残差为0或接近0的时候，此时会进行输出，由于每一棵树会对之前的残差进行计算，那么最后的输出结果不就是和第二棵树的结果相同或者类似吗，因为最后一棵树此时节点的残差值为0或者接近0，和真实值依旧存在误差吗？

老师 xgboost是因为使用了正则化，所以是使用到了梯度下降吗？

老师 特征标准化和特征归一化相同吗

老师这里模型的分数,不仅与超参数有关啊。

比如还和train_test划分比例有关,和cv折数有关,

最后还和超参数的选择有关

那这些比如cv折数啊拆分数据集比例怎么选?(这些也会影响最后的分数)

X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.4,random_state=666；

老师这句代码里的random_state是什么意思

老师，拆分数据集里为什么没有test_size这个参数了

为什么这里不需要拆分数据集?

我为什么我的分词结果跟没分一样？